40 Principal Components

Packages for this chapter:

library(ggbiplot)
library(tidyverse)

40.1 The weather, somewhere

The data in link is of the weather in a certain location: daily weather records for 2014. The variables are:

day of the year (1 through 365)
day of the month
number of the month
season
low temperature (for the day)
high temperature
average temperature
time of the low temperature
time of the high temperature
rainfall (mm)
average wind speed
wind gust (highest wind speed)
time of the wind gust
wind direction

Read in the data, and create a data frame containing only the temperature variables, the rainfall and the wind speed variables (the ones that are actual numbers, not times or text). Display the first few lines of your data frame.
Find five-number summaries for each column by running quantile on all the columns of the data frame (at once, if you can).
Run a principal components analysis (on the correlation matrix).
Obtain a summary of your principal components analysis. How many components do you think are worth investigating?
Make a scree plot. Does this support your conclusion from the previous part?
Obtain the component loadings. How do the first three components depend on the original variables? (That is, what kind of values for the original variables would make the component scores large or small?)
Obtain the principal component scores, for as many components as you think are reasonable, and display the first 20 of them for each component alongside the other variables in your data frame.
Find a day that scores low on component 1, and explain briefly why it came out that way (by looking at the measured variables).
Find a day that scores high on component 2, and explain briefly why it came out that way.
Find a day that scores high on component 3, and explain briefly why it came out high.
Make a biplot of these data, labelling the days by the day count (from 1 to 365). You may have to get the day count from the original data frame that you read in from the file. You can shrink the day numbers to make them overwrite each other (a bit) less.
Looking at your biplot, what do you think was remarkable about the weather on day 37? Day 211? Confirm your guesses by looking at the appropriate rows of your data frame (and comparing with your summary from earlier).

My solutions follow:

40.2 The weather, somewhere

The data in link is of the weather in a certain location: daily weather records for 2014. The variables are:

day of the year (1 through 365)
day of the month
number of the month
season
low temperature (for the day)
high temperature
average temperature
time of the low temperature
time of the high temperature
rainfall (mm)
average wind speed
wind gust (highest wind speed)
time of the wind gust
wind direction

Read in the data, and create a data frame containing only the temperature variables, the rainfall and the wind speed variables (the ones that are actual numbers, not times or text). Display the first few lines of your data frame.

Solution

Read into a temporary data frame, and then process:

my_url <- "http://ritsokiguess.site/datafiles/weather_2014.csv"
weather.0 <- read_csv(my_url)
weather.0

There are lots of columns, of which we only want a few:

(weather.0 %>% select(l.temp:ave.temp, rain:gust.wind) -> weather)

\(\blacksquare\)

Find five-number summaries for each column by running quantile on all the columns of the data frame (at once, if you can).

Solution

I think this is the easiest way. Note the reframe rather than summarize because the “summary” is five numbers rather than one for each column:

weather %>% 
  reframe(across(everything(), \(x) quantile(x)))

This loses the actual percents of the percentiles of the five-number summary (because they are “names” of the numerical result, and the tidyverse doesn’t like names.) I think you can see which percentile is which, though.

Another way to do it is to make a column of column names, using pivot_longer, and then use nest and list-columns to find the quantiles for each variable:

weather %>%
  pivot_longer(everything(), names_to="xname", values_to="x") %>%
  nest_by(xname) %>%
  mutate(q = list(enframe(quantile(data$x)))) %>%
  unnest(q) %>%
  pivot_wider(names_from=name, values_from=value) %>%
  select(-data)

That was a lot of work, but it depends on how you see it when you’re coding it. You should investigate this one line at a time, but the steps are:

create a “long” data frame with one column of variable names and a second with the values for that variable
make mini-data-frames data containing everything but xname: that is, one column x with the values for that variable.
for each mini-data-frame, work out the quantiles of its x. The enframe saves the labels for what percentiles they are.
Unnest this to make a long data frame with one row for each quantile for each variable.
put the variable names in rows and the percentiles in columns.

\(\blacksquare\)

Run a principal components analysis (on the correlation matrix).

Solution

weather.1 <- princomp(weather, cor = T)

\(\blacksquare\)

Obtain a summary of your principal components analysis. How many components do you think are worth investigating?

Solution

summary(weather.1)

Importance of components:
                          Comp.1    Comp.2     Comp.3     Comp.4     Comp.5
Standard deviation     1.7830875 1.4138296 0.74407069 0.38584917 0.33552998
Proportion of Variance 0.5299001 0.3331524 0.09227353 0.02481326 0.01876339
Cumulative Proportion  0.5299001 0.8630525 0.95532604 0.98013930 0.99890270
                            Comp.6
Standard deviation     0.081140732
Proportion of Variance 0.001097303
Cumulative Proportion  1.000000000

The issue is to see where the standard deviations are getting small (after the second component, or perhaps the third one) and to see where the cumulative proportion of variance explained is acceptably high (again, after the second one, 86%, or the third, 95%).

\(\blacksquare\)

Make a scree plot. Does this support your conclusion from the previous part?

Solution

ggscreeplot from ggbiplot:

ggscreeplot(weather.1)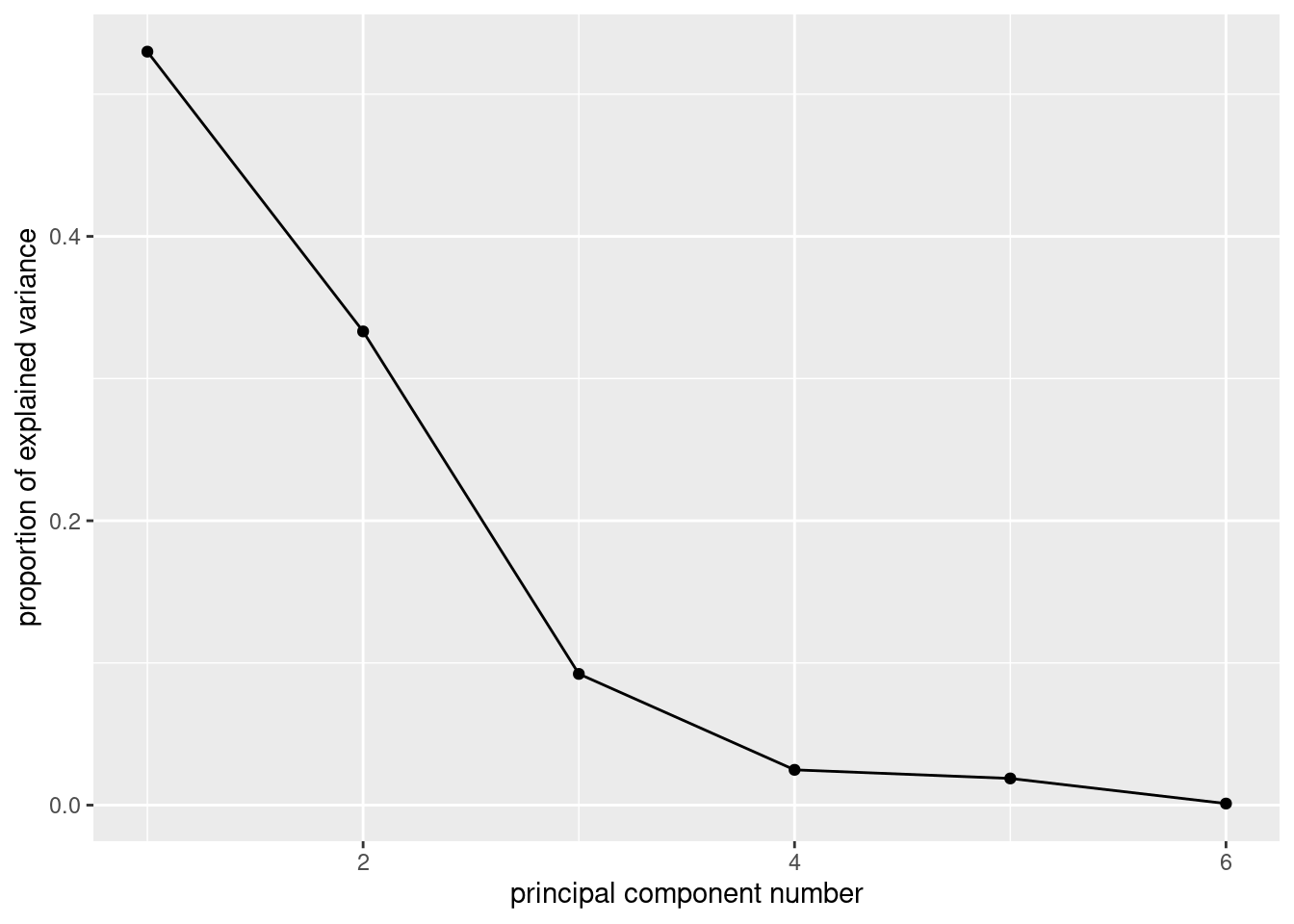

I see elbows at 3 and at 4. Remember you want to be on the mountain for these, not on the scree, so this suggests 2 or 3 components, which is exactly what we got from looking at the standard deviations and cumulative variance explained.

The eigenvalue-greater-than-1 thing (that is, the “standard deviation” in the summary being greater than 1) says 2 components, rather than 3.

\(\blacksquare\)

Obtain the component loadings. How do the first three components depend on the original variables? (That is, what kind of values for the original variables would make the component scores large or small?)

Solution

weather.1$loadings


Loadings:
          Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6
l.temp     0.465  0.348         0.542  0.470  0.379
h.temp     0.510  0.231        -0.576 -0.381  0.458
ave.temp   0.502  0.311                      -0.804
rain      -0.296  0.397  0.853        -0.163       
ave.wind  -0.253  0.560 -0.463  0.357 -0.529       
gust.wind -0.347  0.507 -0.230 -0.492  0.572       

               Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6
SS loadings     1.000  1.000  1.000  1.000  1.000  1.000
Proportion Var  0.167  0.167  0.167  0.167  0.167  0.167
Cumulative Var  0.167  0.333  0.500  0.667  0.833  1.000

1: This component loads mainly (and positively) on the temperature variables, so when temperature is high, component 1 is high. You could also say that it loads negatively on the other variables, in which case component 1 is high if the temperature variables are low and the rain and wind variables are high.
2: This one loads most heavily, positively, on wind: when wind is high, component 2 is high. Again, you can make the judgement call that the other variables also feature in component 2, so that when everything is large, component 2 is large and small with small.
3: This one is a bit clearer. The blank loadings are close to 0, and can be ignored. The main thing in component 3 is rain: when rainfall is large, component 3 is large. Or, if you like, it is large (positive) when rainfall is large and wind is small.

The interpretation here is kind of muffled, because each component has bits of everything. One of the advantages of factor analysis that we see in class later is that you can do a “rotation” so that each variable (to a greater extent) is either in a factor or out of it. Such a varimax rotation is the default for factanal, which I presume I now have to show you (so this is looking ahead):

weather.2 <- factanal(weather, 3, scores = "r")
weather.2$loadings


Loadings:
          Factor1 Factor2 Factor3
l.temp     0.964          -0.230 
h.temp     0.939  -0.203   0.267 
ave.temp   0.992  -0.101         
rain      -0.147   0.604         
ave.wind           0.864         
gust.wind -0.144   0.984         

               Factor1 Factor2 Factor3
SS loadings      2.839   2.131   0.140
Proportion Var   0.473   0.355   0.023
Cumulative Var   0.473   0.828   0.852

These are a lot less ambiguous: factor 1 is temperature, factor 2 is rain and wind, and factor 3 is large (positive) if the high temperature is high or the low temperature is low: that is, if the high temperature was especially high relative to the low temperature (or, said differently, if the temperature range was high).

These factors are rather pleasantly interpretable.

ggbiplot mysteriously doesn’t handle factor analyses, so we have to go back to the base-graphics version, which goes a bit like this:

biplot(weather.2$scores, weather.2$loadings)

Now you see that the factors are aligned with the axes, and it’s very clear what the factors “represent”. (You don’t see much else, in all honesty, but you see at least this much.)

\(\blacksquare\)

Obtain the principal component scores, for as many components as you think are reasonable, and display the first 20 of them for each component alongside the other variables in your data frame.

Solution

Something like this. I begin by turning the component scores (which are a matrix) into a data frame, and selecting the ones I want (the first three):

as_tibble(weather.1$scores) %>%
  select(1:3) %>%
  bind_cols(weather) %>%
  mutate(day = row_number()) -> d
d

I just did the first three scores. I made a column day so that I can see which day of the year I am looking at (later).

\(\blacksquare\)

Find a day that scores low on component 1, and explain briefly why it came out that way (by looking at the measured variables).

Solution

We can do this one and the ones following by running arrange appropriately:

d %>% arrange(Comp.1)

Day 40 has the lowest component 1 score. This is one of the cooler days. Also, there is a largish amount of rain and wind. So low temperature, high rain and wind. Some of the other days on my list were cooler than day 4, but they had less rain and less wind.

\(\blacksquare\)

Find a day that scores high on component 2, and explain briefly why it came out that way.

Solution

d %>% arrange(desc(Comp.2))

Day 37. These are days when the wind speed (average or gust) is on the high side.

\(\blacksquare\)

Find a day that scores high on component 3, and explain briefly why it came out high.

Solution

d %>% arrange(desc(Comp.3))

Day 307. Component 3 was mainly rain, so it is not surprising that the rainfall is the highest on this day.

\(\blacksquare\)

Make a biplot of these data, labelling the days by the day count (from 1 to 365). You may have to get the day count from the original data frame that you read in from the file. You can shrink the day numbers to make them overwrite each other (a bit) less.

Solution

ggbiplot. I did some digging in the help file to figure out how to label the points by a variable and how to control the size of the labels, and I also went digging in the data frame that I read in from the file to get the count of the day in the year, which was called day.count:

ggbiplot(weather.1, labels = weather.0$day.count)

ggbiplot(weather.1, labels = weather.0$day.count, labels.size = 2)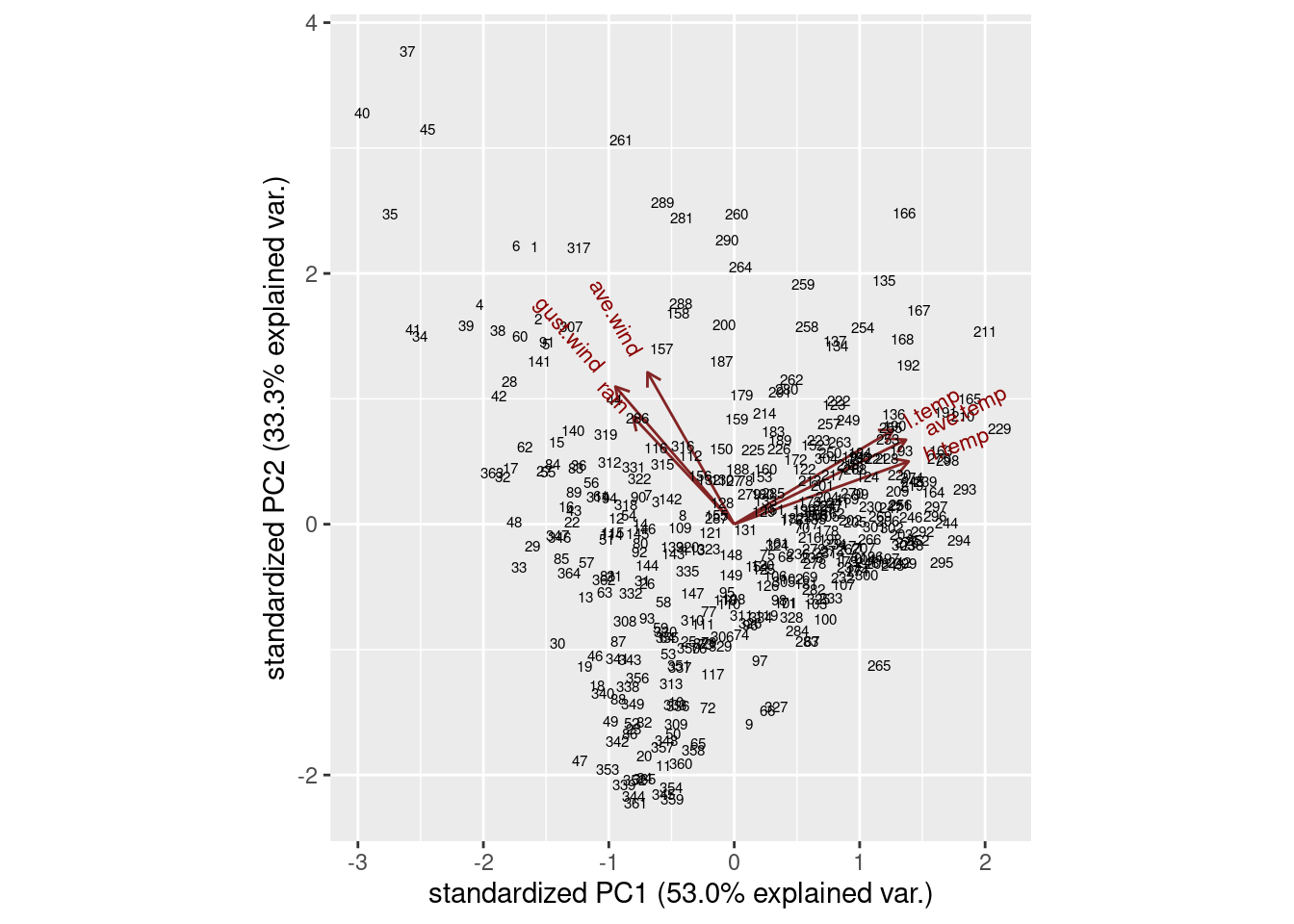

I think the label text is small enough, though you could make it smaller. I’ll be asking you to look at some extreme points in a moment, so those are the only ones you’ll need to be able to disentangle.

The variables divide into two groups: the temperature ones, that point to about 2 o’clock, and the wind and rain ones, that point to about 11 o’clock. These are not straight up or down or across, so they all feature in both components: component 1 is mostly temperature, but has a bit of wind/rain in it, while component 2 is mostly wind/rain with a bit of temperature in it. You might be wondering whether things couldn’t be rotated so that, say, the temperature variables go across and the rain/wind ones go down, which means you’d have a temperature component and a rain/wind component. This is what factor analysis does, and I think I did that earlier (and this is what we found).

\(\blacksquare\)

Looking at your biplot, what do you think was remarkable about the weather on day 37? Day 211? Confirm your guesses by looking at the appropriate rows of your data frame (and comparing with your summary from earlier).

Solution

Day 37 is at the top left of the plot, at the pointy end of the arrows for rain, wind gust and average wind. This suggests a rainy, windy day:

weather %>% slice(37)

Those are high numbers for both rain and wind (the highest for average wind and above the third quartile otherwise), but the temperatures are unremarkable.

Day 211 is towards the pointy end of the arrows for temperature, so this is a hot day:

weather %>% slice(211)

This is actually the hottest day of the entire year: day 211 is highest on all three temperatures, while the wind speeds are right around average (and no rain is not completely surprising).

I can do a couple more. Points away from the pointy end of the arrows are low on the variables in question, for example day 265:

weather %>% slice(265)

This is not really low rain, but it is definitely low wind. What about day 47?

weather %>% slice(47)

This is predominantly low on temperature. In fact, it is kind of low on wind and rain too.¹ This makes sense, because not only is it at the “wrong” end of the temperature arrows, it is kind of at the wrong end of the wind/rain arrows as well.

Having done these by percentile ranks in one of the other

The idea here is that we want to replace all the data values by the percent-rank version of themselves, rather than summarizing them as we have done before. That’s what using an across inside a mutate will do.²

These are:

Day 37: highly rainy and windy (and below average, but not remarkably so, on temperature).
Day 211: the highest or near-highest temperature, no rain but unremarkable for wind. questions, let’s see if we can do that here as well:

weather %>% mutate(across(everything(), \(x) percent_rank(x))) %>% 
    slice(c(37, 211, 265, 47))

Day 265: Lowest for wind (and above Q3 for low temperature and rain).
Day 47: Lowest or near-lowest temperature.

The advantage to doing it this way is that you don’t need a separate five-number summary for each variable; the percentile ranks give you a comparison with quartiles (or any other percentile of interest to you). In case you are wondering where this is: I was doing a presentation using these data to some Environmental Science grad students, and I had them guess where it was. The temperatures for the whole year are warm-temperate, with a smallish range, and sometimes a lot of rain. This suggests a maritime climate. I gave the additional clues of “western Europe” and “this place’s soccer team plays in blue and white striped shirts”. The temperatures have about the right range low-to-high for Britain, but are too warm. Which suggests going south: perhaps Brittany in France, but actually the west coast of the Iberian peninsula: Porto, in northern Portugal, with the weather blowing in off the Atlantic.

\(\blacksquare\)

If you ignore the wind gust, anyway.↩︎
There are also options to keep the original variables, and to give the new ones new names.↩︎